Die Normalverteilung – Ein verborgenes Werkzeug im Qualitätsmanagement

Warum ist fast alles im Leben „normal“ verteilt?
Ob Körpergrößen, Intelligenzquotienten oder Fehlertoleranzen in der Produktion – die Normalverteilung taucht überall auf. Doch was steckt eigentlich hinter dieser berühmten „Glockenkurve“? Finden Sie heraus, warum sie so zentral in Statistik, Wissenschaft und Alltag ist – und was sie dir über die Welt verraten kann.

Autor: Steffen Silbermann

• 3

Was ist die Normalverteilung überhaupt?

Die Normalverteilung beschreibt, wie sich gemessene Werte um einen Durchschnitt herum verteilen. Obwohl auch andere Verteilungsfunktionen genutzt werden, ist diese „Glockenkurve“ die zentrale Grundlage in der modernen Qualitätsstatistik.

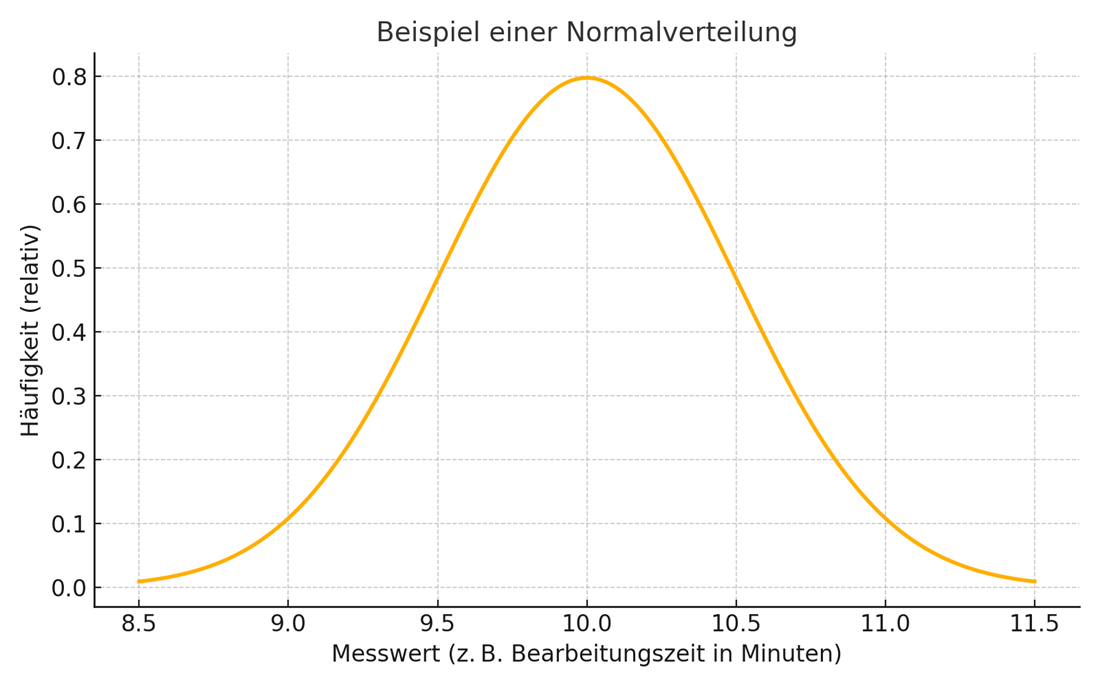
Ein anschauliches Beispiel für eine Normalverteilung: Stellen Sie sich vor, Sie messen die Zeit, die Mitarbeiter für das Verpacken eines Produkts benötigen. Einige sind schneller, andere etwas langsamer, aber die meisten liegen nah am Durchschnitt. Solche Datenreihen sind oft normalverteilt – die Zeiten für einzelne Verpackungsaufträge schwanken symmetrisch um die mittlere Bearbeitungszeit herum.

Eine Normalverteilung entsteht typischerweise dann, wenn viele kleine, unabhängige Einflussgrößen auf ein Ergebnis einwirken – etwa Materialeigenschaften, Werkzeugverschleiß, Umgebungseinflüsse oder menschliche Faktoren – und keine dieser Größen dominiert. Das Zusammenspiel dieser vielen kleinen Variationen führt zur charakteristischen Glockenkurve.

Woher stammt die Normalverteilung?

Die mathematische Grundlage wurde bereits im 18. Jahrhundert gelegt. Der deutsche Mathematiker Carl Friedrich Gauß hat sie entscheidend geprägt – deshalb spricht man auch von der „Gaußschen Normalverteilung“.

Sein Ziel war es ursprünglich, Messfehler in der Astronomie zu beschreiben – heute ist sie ein zentrales Werkzeug in der Statistik.

Wofür kann man die Normalverteilung im Qualitätsmanagement nutzen?

Gerade im Qualitäts-Umfeld geht es darum, Prozesse stabil und vorhersagbar zu machen. Die Normalverteilung hilft dabei in mehrfacher Hinsicht:

• Prozessfähigkeit prüfen: Sie zeigt, wie gut ein Prozess innerhalb der Toleranzen arbeitet. Über Kennzahlen wie Cp und Cpk lässt sich das Verhältnis von Streuung zu Spezifikationsgrenzen analysieren. Wenn die Daten normalverteilt sind, können diese Kennzahlen leicht und aussagekräftig berechnet werden.
• Qualitätsregelkarten: Diese basieren oft auf der Annahme normalverteilter Daten. Damit lassen sich Ausreißer, Trends oder systematische Abweichungen erkennen – und gezielt gegensteuern.
• Fehlerwahrscheinlichkeiten abschätzen: Wenn z. B. bekannt ist, dass die Bearbeitungszeit oder ein Maß normalverteilt ist, lässt sich berechnen, wie wahrscheinlich ein Wert außerhalb der Toleranz liegt – das erleichtert Entscheidungen über Nacharbeit oder Ausschuss.

Woher weiß ich, ob meine Daten normalverteilt sind?

Im Alltag gibt es dafür einfache Hilfsmittel – auch ohne Statistikstudium:

• Histogramme: Diese zeigen die Häufigkeitsverteilung. Ist die Form der Kurve symmetrisch und glockenförmig, ist eine Normalverteilung wahrscheinlich.
• Wahrscheinlichkeitsnetze: In Qualitätssoftware wie Minitab oder mittels Excel-Add-ons lassen sich solche Diagramme erstellen. Wenn die Datenpunkte auf oder nahe der angepassten Verteilungslinie liegen, ist die Verteilung „normal“.
• Verteilungstest: Viele Softwarelösungen bieten auch Verteilungstests an, die prüfen, ob Stichproben aus einer normalverteilten Grundgesamtheit entstammen können. Für die Interpretation sind hierbei dann aber doch einige grundlegende Statistikkenntnisse nötig (Stichworte: Hypothesen und p-Werte).

Fazit: Ein einfaches Modell mit großer Wirkung

Die Normalverteilung ist kein abstraktes Konzept – sie steckt in vielen Prozessen, mit denen sich Lean Manager täglich beschäftigen. Wer sie versteht, kann Prozesse besser bewerten, Risiken abschätzen und Verbesserungen gezielter einleiten.

Auch ohne tiefes mathematisches Wissen lässt sich ihr Nutzen im Qualitätsmanagement effektiv einsetzen – ob bei der Prozessbewertung, der Ursachenanalyse oder der Visualisierung von Streuung.